SparseCraft: Few-Shot Neural Reconstruction
through Stereopsis Guided Geometric Linearization
ECCV 2024
- 1University of Rennes, France
- 2INRIA, CNRS, IRISA, France
SparseCraft learns a linearized implicit neural shape function using multi-view stereo cues, enabling robust training and efficient reconstruction from sparse views.
Abstract
We present a novel approach for recovering 3D shape and view dependent appearance from a few colored images, enabling efficient 3D reconstruction and novel view synthesis. Our method learns an implicit neural representation in the form of a Signed Distance Function (SDF) and a radiance field. The model is trained progressively through ray marching enabled volumetric rendering, and regularized with learning-free multi-view stereo (MVS) cues. Key to our contribution is a novel implicit neural shape function learning strategy that encourages our SDF field to be as linear as possible near the level-set, hence robustifying the training against noise emanating from the supervision and regularization signals. Without using any pretrained priors, our method, called SparseCraft, achieves state-of-the-art performances both in novel-view synthesis and reconstruction from sparse views in standard benchmarks, while requiring less than 10 minutes for training.
Video
How does SparseCraft work?
Taylor Expansion Based Geometric Regularization
We focus on the level set of the Signed Distance Function fθ, where the most crucial knowledge for rendering concentrates. We hypothesize that encouraging the SDF to be as linear as possible there can robustify it against the noise introduced in the training procedure as intuitively, overly complex models are more likely to overfit on noisy samples.
We derive new losses that can achieve this linearization efficiently, while integrating MVS point and normal label supervision seamlessly. We use classical MVS methods such as COLMAP to obtain geometrical cues although incomplete and noisy.
We denote by P the MVS point cloud obtained from input images {Ii}. We note that each sample p ∈ P comes with a normal nMVS(p) and color cMVS(p) estimation. We generate a pool of query points near the surface by sampling around the MVS points following a normal distribution, i.e. {q ∼ N(p, σε I3)}, where the standard deviation σε decreases proportionately with a progressive learning step ε during training, forming the following set of training pairs Q := {(q, p), p = minv∈P ||v - q||2}.
Given a pair (q, p) in Q, we derive from the first-order Taylor polynomial approximation of the SDF fθ around q and p, two losses that encourage the SDF to be as linear as possible near the level set.
The first loss, denoted Ltay(q), is defined as:
The second loss, denoted Ltay(p), is defined as:
Where ∇fθ(p) is the gradient of the SDF at p and nMVS(p) is the normal estimation at p from the MVS point cloud.
The two losses are summed up to form the Taylor expansion based geometric regularization loss and used in addition to the photometric loss and the eikonal loss.
Color Regularization
The color labels provided by MVS are averaged from the input images, so we propose to use them as a supervision to the diffuse component of the radiance function gφ.
our color network consists of two small MLPs gφdiff and gφspec modelling view independent and view dependent radiance respectively:
where Fθ is a feature extracted from the geometry network fθ.
Our color regularization applied at MVS points then can be written as:
Fast Progressive Learning
Our SDF fθ consists of an efficiently CUDA implemented multi-resolution hash encoding followed by a small MLP, and the radiance network gφ consists of two small MLPs. We use an explicit occupancy grid that guides the sampling along rays. This combination allows for fast training.
While progressive learning through positional encoding or learnable features was introduced previously for learning NeRFs from dense and sparse images, we propose here to explore this strategy for SDF based radiance learning in the sparse setting. Differently from previous works, we use the progressive hash encoding to regularize the training in the few shot setting throughout the whole training, rather than its use as a warm-up strategy.
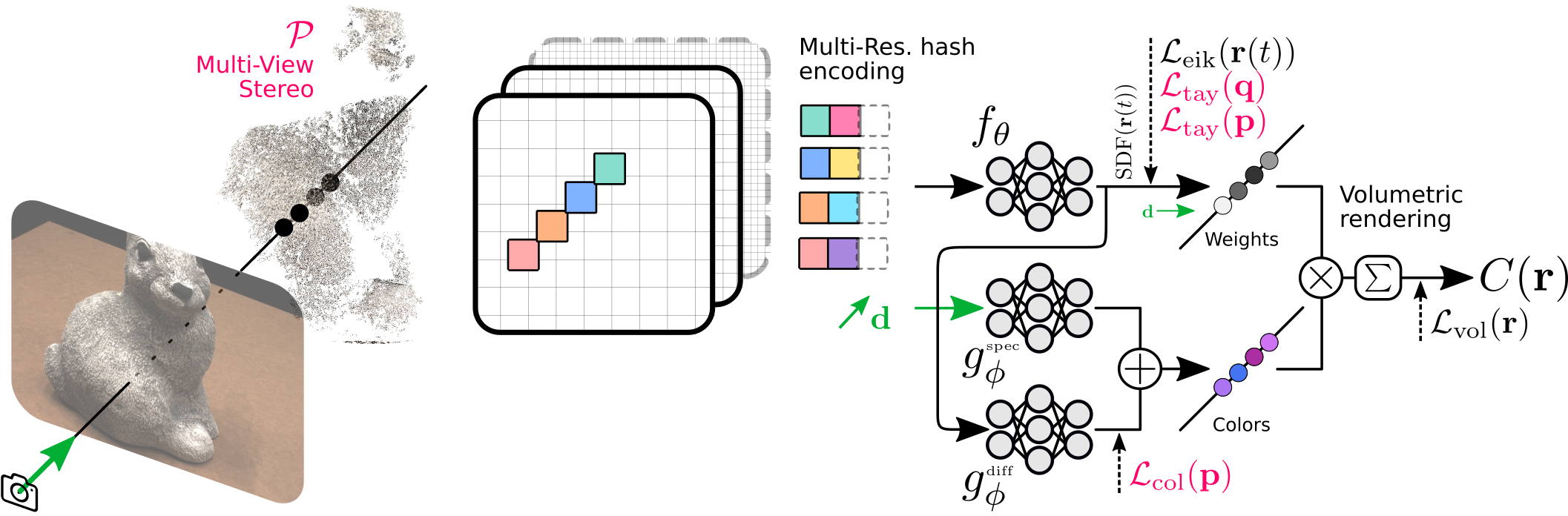
In this toy example, we illustrate the training procedure given 4 samples {r(t)} on a ray r (where the last hash resolution is not active yet). Dashed arrows symbolize losses operating mid-training. SparseCraft leverages differentiable volumetric rendering to learn a SDF based implicit representation given a few images, using MVS cues as regularization (losses in red).
Surface Reconstruction
SparseCraft generates more detailed and complete surfaces compared to previous methods, from sparse input views with as few as 3 input images without any pretrained priors.
Novel View Synthesis
SparseCraft also allows for high-quality novel view synthesis, generating realistic images from novel viewpoints using few input images, surpassing previous NeRF-based methods in the sparse setting.
Citation
If you want to cite our work, please use:
@article{younes2024sparsecraft,
title={SparseCraft: Few-Shot Neural Reconstruction through Stereopsis Guided Geometric Linearization},
author={Mae Younes and Amine Ouasfi and Adnane Boukhayma},
year={2024},
url={https://arxiv.org/abs/2407.14257},
}
Acknowledgements
The website template was borrowed from Michaël Gharbi and MipNeRF360.